What is Critical Value Test of Hypothesis?
Critical Value Testing
The critical value for a test of hypothesis relies upon a test statistic, that is unique to the type of test, and the significance level, α, which defines the sensitivity of the test.
A rate of α = 0.05 method that the null hypothesis is rejected 5 % of the time even as it’s far in fact true.
The choice of α is pretty arbitrary, despite the fact that workout values of 0.1, 0.05, and 0.01 are common. Critical values are essentially cut-off values that define regions in which the test statistic isn’t always going to lie; for example, an area in which the essential rate is surpassed with threat α if the null hypothesis is true.
The null hypothesis is rejected if the test statistic lies interior this area that is frequently referred to as the rejection area(s). Critical values for unique checks of the hypothesis are tabled in financial disaster 1.
https://criticalvaluecalculator.com
How to Determine a p-Value When Testing a Null Hypothesis
When you check speculation approximately a populace, you may use your check statistic.
Determine whether or not to reject the null speculation, H0. You make this selection with the aid of using developing with a range, known as a p-fee.
A p-fee is an opportunity related to your vital fee. The vital fee relies upon the opportunity you’re taking into consideration a Type I blunders.
It measures the danger of having outcomes at the least as sturdy as yours if the declare (H0) have been true.
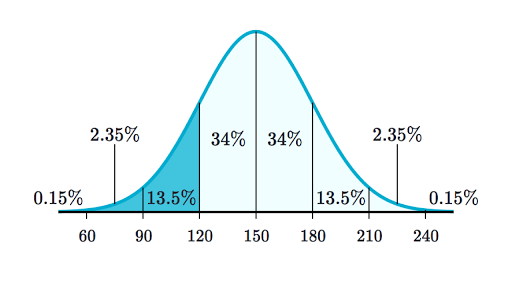
The following discern indicates the places of a check statistic and their corresponding conclusions.
Suppose you’re trying out a declare that the proportion of all girls with varicose veins is 25%, and your pattern of a hundred girls had 20% with varicose veins.
Then the pattern percentage p=0.20. The preferred blunders on your pattern percent are the rectangular root of p(1-p)/n which equals 0.04 or 4%.
These calculations come up with a check statistic (preferred score) of –0.05 divided with the aid of using 0.04 = –1.25. This tells you that your pattern outcomes and the populace declare in H0 are 1.25 preferred mistakes apart; in particular, your pattern outcomes are 1.25 preferred mistakes under the declare.
Note: If you were trying out the -sided alternative,
the p-fee might be 2 ∗ 0.1056, or 0.2112.
The Critical Value approach
By making use of the critical value approach it’s far determined, whether or not or now no longer the found check statistic is extra severe than a described vital fee.
Therefore the found check statistic (calculated on the idea of pattern records) is in comparison to the vital fee, a few sort of cutoff fees. If the check statistic is extra severe than the vital fee, the null speculation is rejected.
If the check statistic isn’t always as severe because of the critical value, the null speculation isn’t always rejected. The vital fee is computed primarily based totally on the given importance stage and the sort of opportunity distribution of the idealized version. The vital fee divides the location beneath neath the opportunity distribution curve in rejection vicinity(s) and in non-rejection vicinity.
In a -sided check the null speculation is rejected if the check statistic is both too small or too large. Thus the rejection vicinity for one of these check includes parts: one at the left and one at the proper
The P-Value Approach
For the p-fee approach, the likelihood (p-fee) of the numerical fee of the check statistic is in comparison to the required importance stage (α” role=”presentation” style=”display: inline; line-height: everyday; word-spacing: everyday; overflow-wrap: everyday; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;”>αα) of the speculation check.
The p-fee corresponds to the opportunity of watching pattern records at the least as severe because of the truly acquired check statistic. Small p-values offer proof towards the null speculation. The smaller (towards 0) the p-fee, the more potent is the proof towards the null speculation.
In consequence, with the aid of using understanding the p-fee any preferred stage of importance can be assessed. For example, if the p-fee of a speculation check is 0.01, the null speculation may be rejected at any importance stage large than or same as 0.01.
It isn’t always rejected at any importance stage smaller than 0.01. Thus, the p-fee is usually used to assess the energy of the proof towards the null speculation without connection with the important stage.





